Gato: Algorithms: Shortest Path
Computing a Shortest Path on Euclidian Graphs
The algorithms in the following example are part of CATBox. NOTE: The screenshots are old and from Gato running on Solaris/Openwin.
In this example we will demonstrate how Gato allows students to learn more about developing better algorithms by making use of problem-specific knowledge.
One fundamental problem in algorithmic graph theory is finding the shortest path between two vertices in a graph. That is, given a set of vertices and a set of weighted edges where the weight on an edge corresponds to the distance between the vertices it connects, find a path such that the sum of all weights of edges on the path is minimal.
If the graph is Euclidean (i.e., the distance between vertices is simply the Euclidean distance between their positions in a two-dimensional embedding), then the standard algorithm can be improved.
By running the standard algorithm on several different graphs, students observe that the shortest path is always "close" to a straight line between the two vertices. This observation can then be used to investigate how the standard algorithm selects which vertex to visit next by single-stepping through the algorithm. This may lead students to conclude that visiting vertices which are too "far away" from a straight line is unnecessary.
This conclusion can be formalized mathematically in terms of a simple inequality and directly implemented in Gato (basically by changing one line). The modified algorithm can then be run again to experimentally verify the student's argument and -- in case of subtle errors -- to provide insights, again by single-stepping through the algorithm, into the source of error.
Computing a shortest path
Loading a graph and an algorithm: Both graphs and algorithms are loaded into Gato during run-time. The user may select the files he/she wants using dialogs typical for the specific platform.
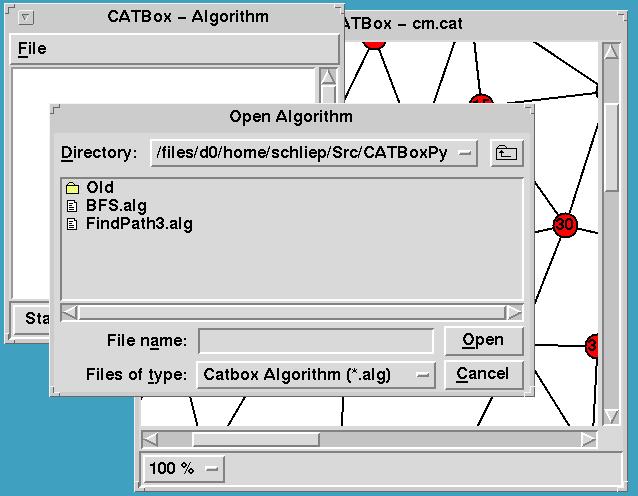
Running an algorithm: After a graph and an algorithm have been loaded, the Start button is used to let the algorithm run until termination, since we are only interested in looking at shortest paths.
Looking at shortest paths: Here we see what a student would
observe during several runs. In the case of Euclidean graphs, where
the weight of an egde corresponds to the Euclidean distance between
the vertices it connects, the shortest path between two vertices
(here: top left and bottom right) is "close" to a straigt line between
the two vertices. Note, that all vertices and all edges have been
visited. 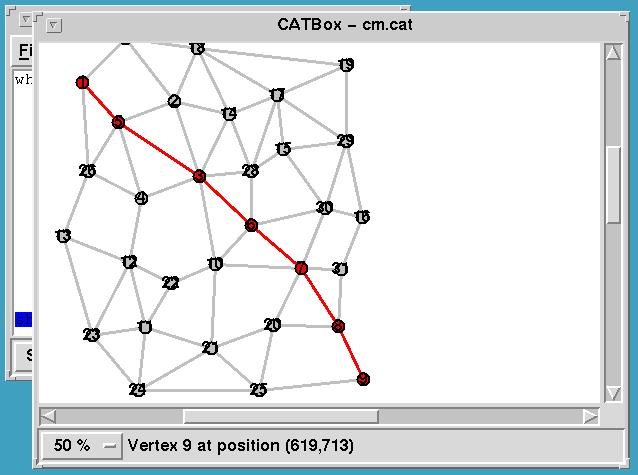
Examining choice of edges
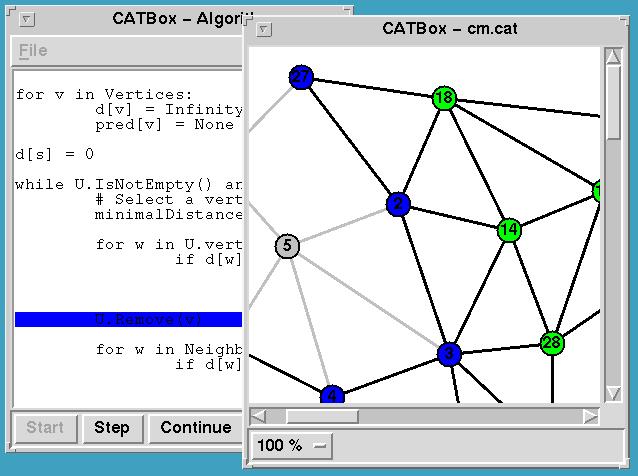
Breakpoints: One feature for investigating an algorithm are
breakpoints; i.e., to specify a line of the source code at which
execution is halted. Users can set and remove breakpoints (displayed
as red lines) by clicking on them with the mouse. Once started, the
algorithm will halt, when it reaches the line. The user can then
observe the state and either use the Stop button to quit or use Cont
to continue execution.
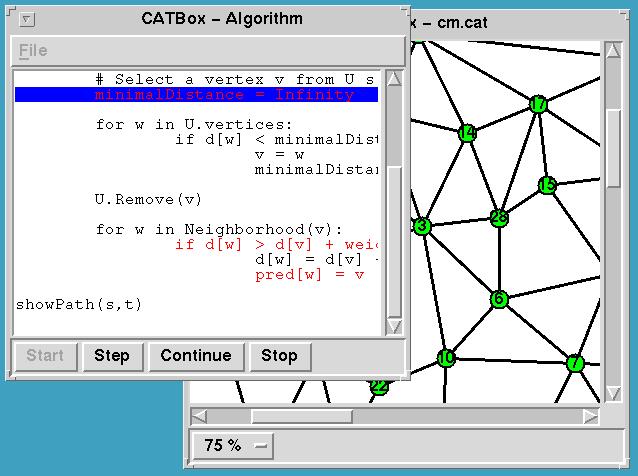
Single-stepping: Alternatively, the user can choose to step --
i.e., to execute one line at a time -- through the algorithm.
Observing choice: By single-stepping through the lines of code
which choose the next vertex visited by the algorithm, the student can
observe that in this instance several alternatives can be ruled out
due to a simple geometric consideration (which is obvious to humans
but not to algorithms): a straight line is the shortest connection
between two points (here: of the neighbors of vertex 6, certainly
vertex 7 will be on a shortest path to vertex 9, but not vertex 10)

Changing the algorithm
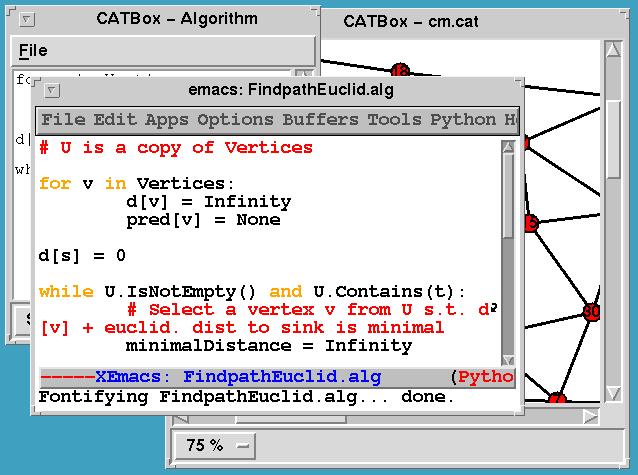
Editing algorithms: The user can use an external editor of
his/her choice for changing algorithms.
Comparing results
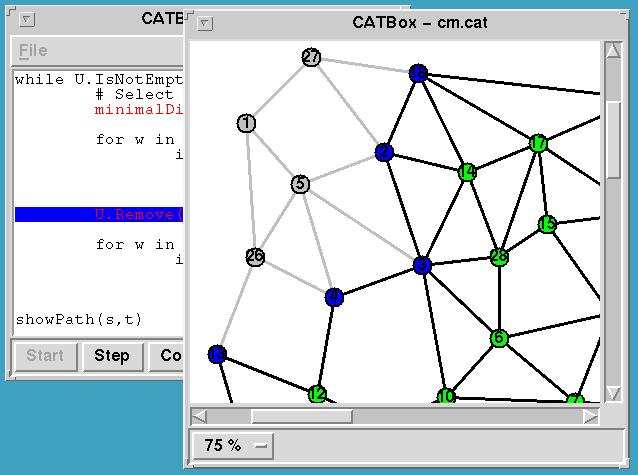
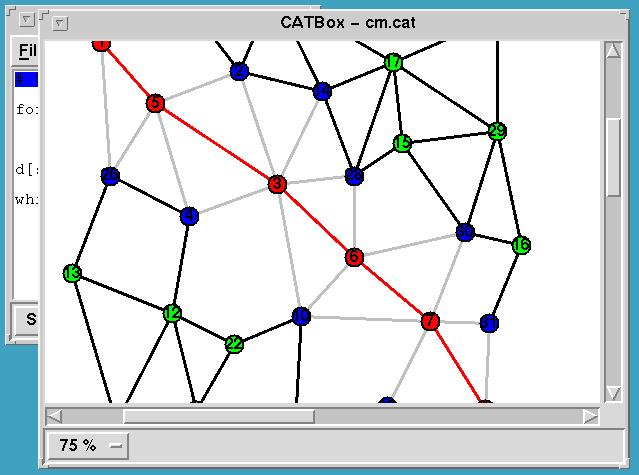
Running the modified algorithm: By running the modified
algorithm the student can heuristically examine the speed-up the
changes produced. The modified algorithm visits a far smaller number
of edges and vertices (traversed edges are displayed in grey).
Checking for errors: In case of errors in the modified
algorithm, students can use breakpoints and single-stepping and/or
modified graphs to investigate under which circumstances errors
occured. 